Фракталы. Что же это такое?
Опубликовано ssu-filippov в 6 июня, 2011 - 06:00
Редакция NNN случайно наткнулась на весьма интересный
материал, представленный в блоге пользователя xtsarx, посвященный
элементам теории фракталов и ее практическому
применению. Как известно, терия фракталов играет далеко не последнюю
роль в физике и химии наносистем. Внеся свою лепту в этот добротный
материал, изложенный на языке, доступном для широкого круга читателей и
подкрепленный обильным количеством графического и даже видео материала,
мы представляем его Вашему вниманию. Надеемся, что читателям NNN этот
материал будет интересным.
Природа так загадочна, что чем больше изучаешь ее, тем больше
вопросов появляется… Ночные молнии – синие «струи» ветвящихся разрядов,
морозные узоры на окне, снежинки, горы, облака, кора дерева – все это
выходит за рамки привычной евклидовой геометрии. Мы не можем описать
камень или границы острова с помощью прямых, кружков и треугольников. И
здесь нам приходят на помощь фракталы. Что же это за знакомые незнакомцы?
«Под микроскопом он открыл, что на блохе
Живет блоху кусающая блошка;
На блошке той блошинка-крошка,
В блошинку же вонзает зуб сердито
Блошиночка, и так ad infinitum». Д.Свифт.
Немного из истории
Первые идеи фрактальной геометрии возникли в
19 веке. Кантор с помощью простой рекурсивной (повторяющейся) процедуры
превратил линию в набор несвязанных точек (так называемая Пыль Кантора).
Он брал линию и удалял центральную треть и после этого повторял то же
самое с оставшимися отрезками.
 Рис. 1. Кривая пеано 1,2–5 итерации. Рис. 1. Кривая пеано 1,2–5 итерации.
Пеано нарисовал особый вид линии. Пеано поступил следущим образом:
На первом шаге он брал прямую линию и заменял ее на 9 отрезков длинной в
3 раза меньшей, чем длинна исходной линии. Далее он делал то же самое с
каждым отрезком получившейся линии. И так до бесконечности. Ее
уникальность в том, что она заполняет всю плоскость. Доказано, что для
каждой точки на плоскости можно найти точку, принадлежащую линии Пеано.
Кривая Пеано и пыль Кантора выходили за рамки обычных геометрических
объектов. Они не имели четкой размерности. Пыль Кантора
строилась вроде бы на основании одномерной прямой, но состояла из точек
(размерность 0). А кривая Пеано строилась на основании одномерной
линии, а в результате получалась плоскость. Во многих других областях
науки появлялись задачи, решение которых приводило к странным
результатам, на подобие описанных выше (Броуновское движение, цены на
акции). Каждый из нас может проделать эту процедуру…
Отец Фракталов
Вплоть до 20 века шло накопление данных о таких странных объектах,
без какой-либо попытки их систематизировать. Так было, пока за них не
взялся Бенуа Мандельброт – отец современной фрактальной геометрии и слова фрактал.
 Рис. 2. Бенуа Мандельброт. Рис. 2. Бенуа Мандельброт.
Работая в IBM математическим аналитиком, он изучал шумы в электронных
схемах, которые невозможно было описать с помощью статистики.
Постепенно сопоставляя факты, он пришел к открытию нового направления в
математике – фрактальной геометрии.
Термин «фрактал» Б.Мандельброт ввёл в 1975 г.. Согласно Мандельброту, фракталом (от лат. «fractus» – дробный, ломанный, разбитый) называется структура, состоящая из частей, подобных целому. Свойство самоподобия резко отличает фракталы от объектов классической геометрии. Термин самоподобие означает наличие тонкой, повторяющейся структуры, как на самых малых масштабах объекта, так и в макромаштабе.
 Рис. 3. К определению понятия «фрактал». Рис. 3. К определению понятия «фрактал».
Примерами самоподобия служат: кривые Коха, Леви, Минковского, треугольник Серпиньского, губка Менгера, дерево Пифагора и др.
С математической точки зрения, фрактал – это, прежде всего, множество с дробной (промежуточной, «не целой») размерностью.
В то время как гладкая евклидова линия заполняет в точности одномерное
пространство, фрактальная кривая выходит за пределы одномерного
пространства, вторгается за границы в двумерное пространство.Таким
образом, фрактальная размерность кривой Коха будет находиться между 1 и
2. Это, прежде всего, означает, что у фрактального объекта невозможно
точно измерить его длину! Из этих геометрических фракталов очень
интересным и довольно знаменитым является первый – снежинка Коха.
 Рис. 4. К определению понятия «фрактал». Рис. 4. К определению понятия «фрактал».
Строится она на основе равностороннего треугольника.
Каждая линия которого заменяется на 4 линии каждая длиной в 1/3
исходной. Таким образом, с каждой итерацией длинна кривой увеличивается
на треть. И если мы сделаем бесконечное число итераций – получим
фрактал – снежинку Коха бесконечной длины. Получается, что наша
бесконечная кривая покрывает ограниченную площадь. Попробуйте сделать то
же самое методами и фигурами из евклидовой геометрии.
Размерность снежинки Коха
(при увеличении снежинки в 3 раза ее длина возрастает в 4 раза) D=log(4)/log(3)=1.2619.
О самом фрактале
Фракталы находят все большее и большее применение в науке и технике.
Основная причина этого заключается в том, что они описывают реальный мир
иногда даже лучше, чем традиционная физика или математика. Можно до
бесконечности приводить примеры фрактальных объектов в природе, – это и
облака, и хлопья снега, и горы, и вспышка молнии, и наконец, цветная
капуста. Фрактал как природный объект – это вечное непрерывное движение,
новое становление и развитие.
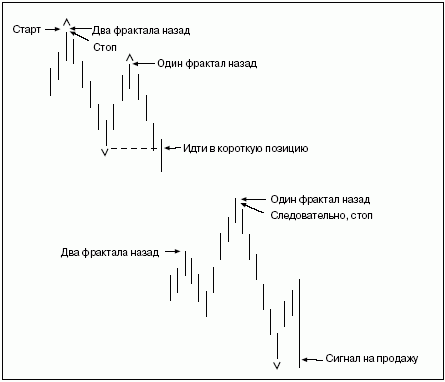 Рис. 5. Фракталы в экономике. Рис. 5. Фракталы в экономике.
Кроме того, фракталы находят применение в децентрализованных компьютерных сетях и «фрактальных антеннах».
Весьма интересны и перспективны для моделирования различных
стохастических (не детерминированных) «случайных» процессов, так
называемые «броуновские фракталы». В случае нанотехнологий фракталы тоже играют важную роль, поскольку из-за своей иерархической самоорганизации многие наносистемы обладают нецелочисленной размерностью, то есть являются по своей геометрической, физико-химической или функциональной природе фракталами. Например, ярким примером химических фрактальных систем являются молекулы «дендримеров».
Кроме того, принцип фрактальности (самоподобной, скейлинговой
структуры) является отражением иерархичности строения системы и поэтому
является более общим и универсальным, чем стандартные подходы к описанию
строения и свойств наносистем.
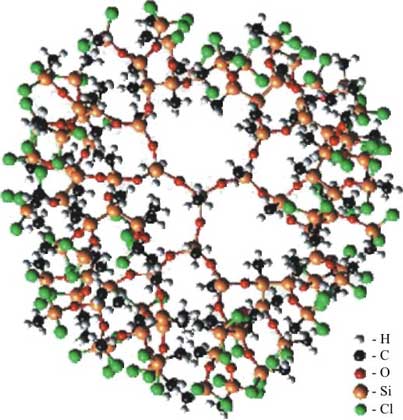 Рис. 6. Молекулы «дендримеров». Рис. 6. Молекулы «дендримеров».
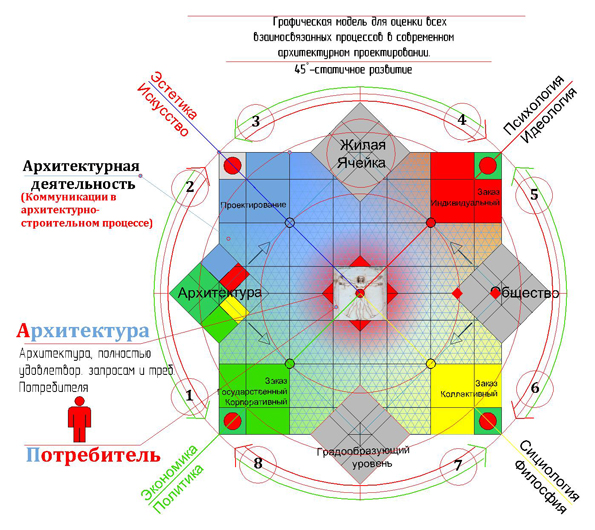 Рис. 7. Графическая модель коммуникации в архитектурно-строительном
процессе. Первый уровень взаимодействия с позиций микропроцессов.
Рис. 7. Графическая модель коммуникации в архитектурно-строительном
процессе. Первый уровень взаимодействия с позиций микропроцессов.
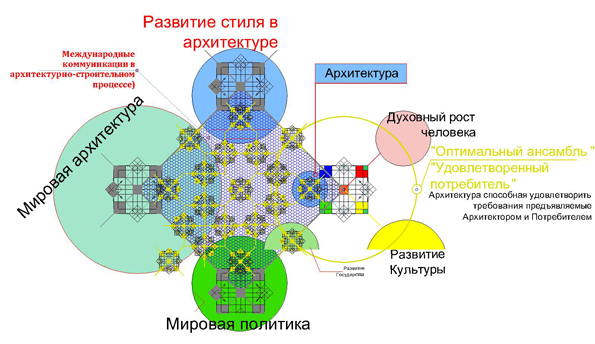 Рис. 8. Графическая модель коммуникации в архитектурно-строительном
процессе. Второй уровень взаимодействия с позиций макропроцессов
(фрагмент модели).
Рис. 8. Графическая модель коммуникации в архитектурно-строительном
процессе. Второй уровень взаимодействия с позиций макропроцессов
(фрагмент модели).
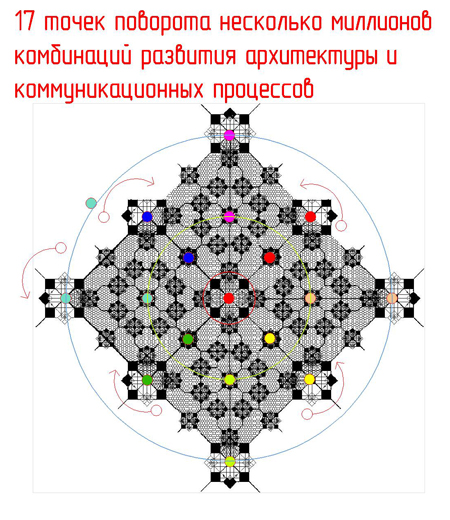 Рис. 9. Графическая модель коммуникации в архитектурно-строительном
процессе. Второй уровень взаимодействия с позиций макропроцессов (модель
целиком)
Рис. 9. Графическая модель коммуникации в архитектурно-строительном
процессе. Второй уровень взаимодействия с позиций макропроцессов (модель
целиком)
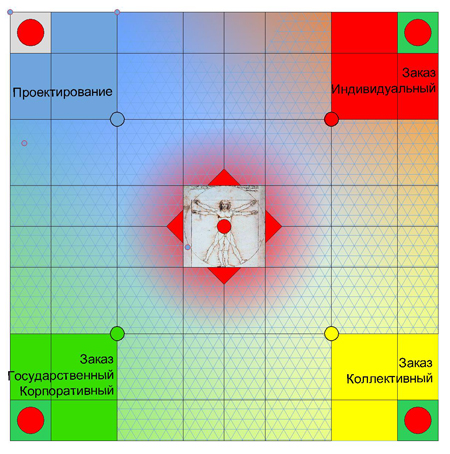 Рис. 10. Плоскостное развитие графической модели. Первое гомеостатичное состояние. Рис. 10. Плоскостное развитие графической модели. Первое гомеостатичное состояние.
Фракталы и золотое сечение
«Фракталы» часть 1
«Фракталы» часть 2
«Фракталы» часть 3
«Фракталы» часть 4
«Фракталы» часть 5
Фотогалерея красивых и необычных фракталов
 Рис. 11. Рис. 11.
 Рис. 12. Рис. 12.

- сточник(и):
1. Блог xtsarx
http://www.nanonewsnet.ru/articles/2011/fraktaly-chto-zhe-eto-takoe
| 








